Ptolemy Hierarchical Orthogonal Multi-Attribute Solver (PtHOMAS)

Download

PtHOMAS is part of the Ptolemy II project. Users can try out the software and see the source code by downloading a nightly build. See the ptexternal page for access. PtHOMAS code is referred to as Ontologies within vergil and the source code is located in $PTII/ptolemy/data/ontologies.

About

Ptolemy Hierarchical Orthogonal Multi-Attribute Solver (PtHOMAS) is a collaborative project with CHESS partner Bosch through the Bosch Research and Technology Center with additional funding from the Army Research Office in connection with the OSD Software-Intensive Systems Producibility Initiative. This project also has applications in the NAOMI collaboration with CHESS partner Lockheed-Martin.

This project is focused on enhancing model-based design techniques with the ability to include in models semantic information about data (what the data means), to check consistency in the usage of data across models, and to optimize models based on inferences made about the meaning of the data.

The approach is to build on classical data type systems, which address this problem up to a point. It is easy to check, for example, whether two models agree that a variable represents an integer value. But additional meaning like the units and the semantic interpretation of the data is not captured in the type system. An organization of such meaning is referred to in computer science as a data ontology.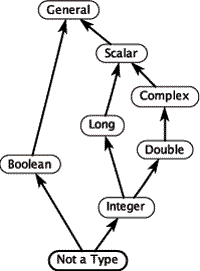

In classical type systems, the relationship between types form a partial order, or more specifically, a mathematical lattice, as shown above for small subset of a typical type system. Type checking and type inference algorithms are based on efficient algorithms for solving systems of inequalities over such partial orders.

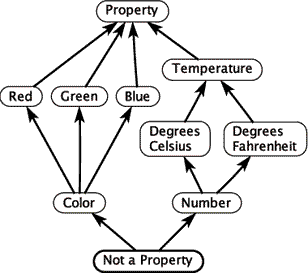
A data ontology can be similarly constructed as a lattice, as shown in the example above. In this example, each node in the ontology specifies an interpretation of a piece of data and the relations between nodes indicate "is a" relationships between these interpretations. In the PtHOMAS project, we associate such ontologies with models and apply consistency checks, inference algorithms, and model optimizations based on the results of the inference.

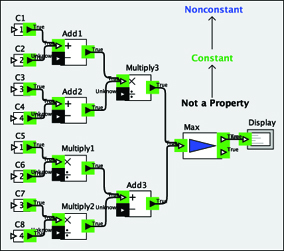
The above Ptolemy II model, for example, has a simple 3-element lattice associated with it (NotAProperty -> Const -> Nonconstant), and based on inference results, can be automatically transformed to the much simpler model shown below.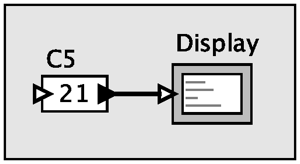

Publications

Ben Lickly, Charles Shelton, Elizabeth Latronico, Edward A. Lee. A Practical Ontology Framework for Static Model Analysis, EMSOFT '11: Proceedings of the Ninth International Conference on Embedded Software, ACM, 23-32, October 10, 2011. Presentation slides.
Charles Shelton, Elizabeth Latronico, Ben Lickly. Static Analysis using the Ptolemy II Ontologies Package, Talk or presentation, February 16, 2011; Presented at the Ninth Biennial Ptolemy Miniconference, Berkeley, CA.
Edward A. Lee, Ben Lickly, Jackie Man-Kit Leung, Thomas Mandl, Elizabeth Latronico, Charles Shelton, Stavros Tripakis. Ensuring Correct Composition of Components using Lattice-based Ontologies, Talk or presentation, 11, October, 2009; WFCD - Foundations and Applications of Component-based Design in Conjunction with ES Week, Grenoble, France, October 11, 2009.
Jackie Man-Kit Leung, Thomas Mandl, Edward A. Lee, Elizabeth Latronico, Charles Shelton, Stavros Tripakis, Ben Lickly. Scalable Semantic Annotation using Lattice-based Ontologies, 12th International Conference on Model Driven Engineering Languages and Systems, ACM/IEEE, 393-407, October 8, 2009

Mailing lists and discussion forums may be found under the pthomas link above.